One-Sample T-Test

There are three main types of t-test:

One-sample t-test: compare a sample mean to a reference mean value.
Independent samples t-test: compare the means of two independent groups.
Paired samples t-test: compare two means taken from the same group under different conditions.

Mean Goals Conceded in the Premier League

Let’s say someone states ‘a defender in the Premier League concedes 1 goal a game on average’. I would be able to test if this is true using a one-sample t-test on a sample of players from the 2024-2025 season!

Here the null hypothesis is that defenders in the Premier League concede a mean of 1 goal per game.
The alternative hypothesis is that defenders in the Premier League on average concede more than 1 goal per game, or less than 1 goal per game.

Getting Data

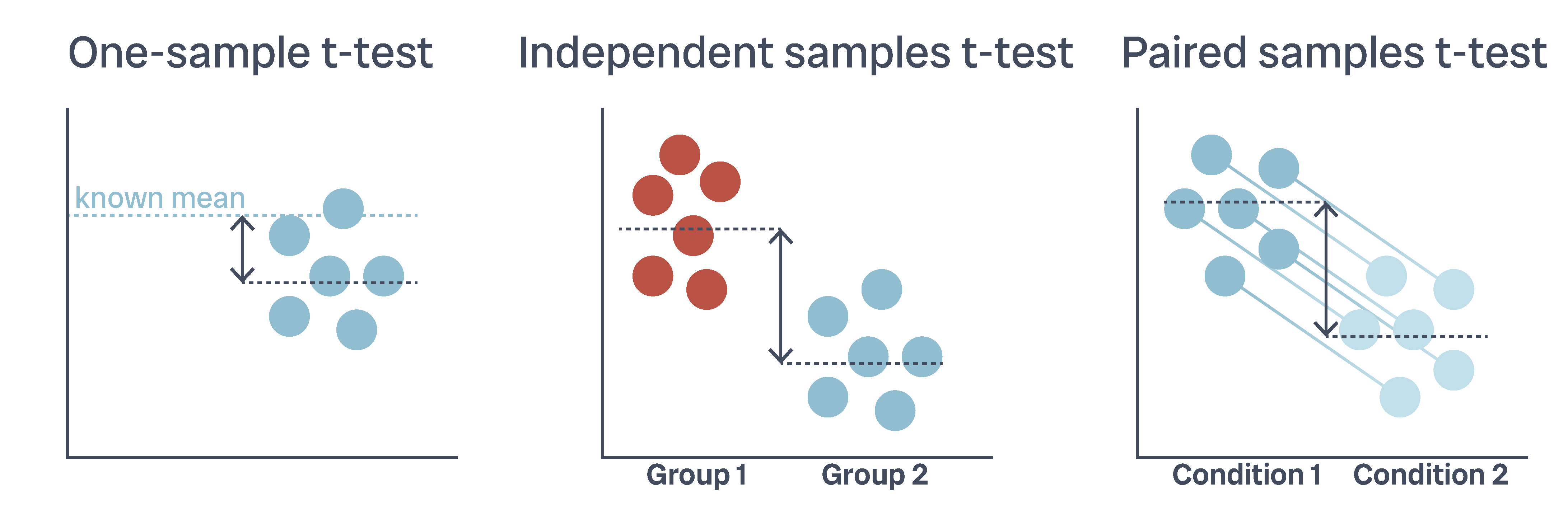
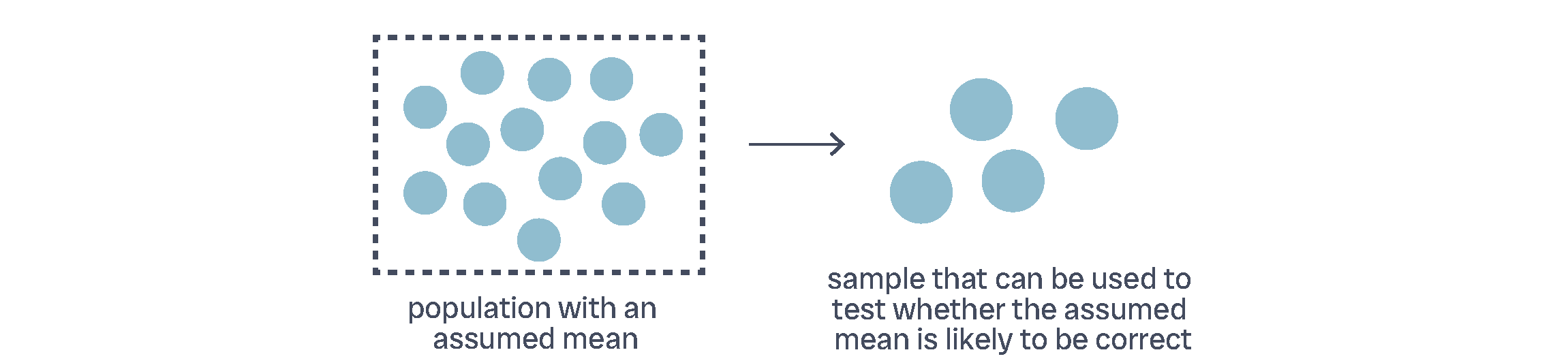
# Load packages
library(tidyverse)

# Read data
Path <- '/Users/alicesmail/Desktop/Programming/GitHubPage/FPL/2024-2025-Data/'
PlayerData <- read_csv(paste0(Path, "FPL-Gameweeks-29.csv"))

First I can load some data from this season, and summarise the data to get the mean goals conceded per 90 minutes for each player. Importantly I have also filtered for defenders and goalkeepers that have started at least 5 games.

# Get goals scored for each player
GoalsCon <- PlayerData %>% group_by(web_name, position, team_name) %>% 
  summarise(goals_conceded=sum(goals_conceded), minutes=sum(minutes), starts=sum(starts)) %>%
  filter(starts>=5, position%in%c('DEF','GKP')) %>%
  mutate(mean_goals_conceded=goals_conceded/minutes*90)

Next I can plot a histogram of this data. I can see that the data is approximately normally distributed, and the mean is around 1.6. So the mean goals conceded is higher than 1 in this sample, but the t-test can help me decide if it is a meaningful difference that would help prove that the statement ‘a defender in the Premier League concedes 1 goal a game on average’ is incorrect.

ggplot(GoalsCon, aes(x=mean_goals_conceded))+
  geom_histogram(fill='#90bdcf')+
  theme_classic()+
  theme(text=element_text(family='Radio Canada Big',size=14))+
  labs(x='Goals Conceded per Player', y='Player Count')+
  geom_vline(xintercept=mean(GoalsCon$mean_goals_conceded), colour='black', linetype='dashed')

Performing a T-Test

Next I can calculate a t-statistic, using the sample count (154), population mean (1), sample mean (1.6), and the sample standard deviation (0.5). I get a t-statistic of 15, which is quite extreme! Because I am testing whether the sample mean is different to the population mean of 1, I am doing a two-tailed t-test - if I wanted to test if the sample mean is larger or smaller than the population mean, I could use a one-tailed test.

# Calculate the t-statistic
tStat <- (mean(GoalsCon$mean_goals_conceded)-1)/(sd(GoalsCon$mean_goals_conceded)/sqrt(nrow(GoalsCon)))
tStat

# T-distribution plot
ggplot(data.frame(x=c(-10, 10)), aes(x=x)) +
  stat_function(fun=dt, args=list(df=nrow(GoalsCon)-1)) +
  theme_classic() +
  geom_vline(xintercept=c(tStat, -tStat), colour='#ff5900')+
  labs(x='',y='')

## [1] 14.90358

Now I can obtain the p-value from the t-statistic. This is equivalent to getting the area under the curve from x=-Inf to -15 and 15 to Inf. The p-value I get is really tiny, meaning this difference is unlikely to be due to chance, and that the null hypothesis can be rejected.

# Calculate p-value manually
2 * pt(abs(tStat), nrow(GoalsCon)-1, lower.tail=FALSE)

## [1] 4.033147e-32

The t.test function in R also does all of this in one go!

t.test(GoalsCon$mean_goals_conceded, mu=1, alternative="two.sided")

## One Sample t-test
## data:  GoalsCon$mean_goals_conceded
## t = 14.904, df = 161, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 1
## 95 percent confidence interval:
## 1.489268 1.638735
## sample estimates:
## mean of x 1.564002

Summary

Here I have used a one-sample t-test to test the hypothesis that Premier League defenders concede 1 goal on average per game. In my sample I have found a mean of 1.6 goals conceded per game, which is significantly different from the popluation mean of 1, so I would reject this as a null hypothesis.